In genere, le specifiche ed i problemi riguardanti la registrazione, così come la riproduzione dei suoni in formato digitale, hanno sempre qualcosa a che fare con questo misterioso fenomeno che prende il nome di campionamento. Per quale motivo si campiona un segnale? Cos’è in realtà il campionamento? Quali sono i vantaggi impliciti nel campionare un segnale?In questa sezione si tenterà di dare una panoramica generale circa il significato matematico del campionamento di un segnale.
Ci scusiamo in anticipo se il linguaggio utilizzato risulterà troppo specifico, ma le nozioni esposte torneranno utili in vista dei prossimi articoli di questa rubrica.
Innanzitutto cos’è un segnale?
Un segnale determinato è una funzione che assume valori ben precisi e noti nel dominio di definizione. Per dirla in parole più semplici, una funzione matematica che associa un numero conosciuto nell’ambito del mondo in cui opera è definita come “segnale”.
Per esempio, la funzione che definisce un’onda acustica è un segnale il cui campo di definizione è il tempo: ad ogni istante l’onda acustica presenterà caratteristiche di altezza note.
Esistono due tipi di segnali determinati a seconda del campo di esistenza:
- Segnali continui, il cui insieme di definizione è un intervallo o tutto l’asse dei numeri reali.
- Segnali discreti, il cui insieme di definizione è formato da istanti di tempo discreti, equamente intervallati.
Inoltre, un segnale determinato può essere a valori discreti o a valori continui: nel primo caso, il segnale può assumere, in tutti gli istanti dell’insieme di definizione, solo valori discreti (anche infiniti); nel secondo caso, il segnale può assumere un qualsiasi valore in un intervallo o in tutto l’insieme dei numeri reali.
D’ora in poi ci si riferirà ai segnali continui con la funzione S(t), mentre ai segnali discreti con Sc(T).
Per dare un’idea più precisa riguardo a ciò di cui si sta parlando, potremo dire che un segnale analogico è un segnale continuo, mentre la sua “traduzione” numerica (in “digitale”) è un segnale discreto.
La trasmissione di un segnale analogico, ossia un segnale continuo nel tempo che assume valori continui esso stesso, si rende indispensabile in fase di registrazione o anche soltanto di processazione del segnale. Un particolare tipo di trasmissione, che è poi quello che ci interessa in questo caso, è la trasmissione in forma digitale, ovvero come sequenza di bit. Questo tipo di trasmissione è quella che si realizza quando vogliamo registrare tramite HD recording o quando si usa un filtro digitale per l’equalizzazione o l’effettazione in generale del suono.
La trasmissione digitale viene fatta in forma numerica. Per questo motivo lo schema di trasmissione da considerare deve essere tale da permettere la codifica del segnale in forma binaria.
Se si utilizza una fonte analogica per la riproduzione del segnale numerico l’operazione da attuare è quella di decodifica. Quindi il primo passaggio da compiere sul nostro segnale S(t) è appunto il campionamento. La sua funzione è quella di generare valori numerici (campioni) di interpretazione che poi consentiranno l’elaborazione software e la ricostruzione del segnale stesso, tanto più fedele quanto più il campionamento è applicato in maniera corretta.
Un primo schema di trasmissione del segnale può essere rappresentato tramite il seguente blocco:
In uscita dal blocco “campionatore”, avremo i campioni del segnale di partenza. Il campionamento del segnale ci garantisce, sotto opportune condizioni, una certa fedeltà al segnale analogico trasmesso.
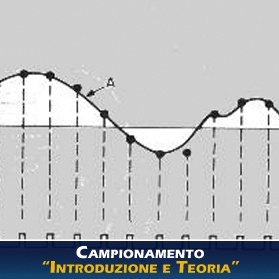
Vediamo ora cosa succede effettuando il campionamento di un segnale e sotto quali condizioni è possibile ricostruire tale segnale a partire dai suoi campioni.
Innanzitutto dovremo tenere presente che, se si vuole “discretizzare” un segnale continuo, dovremo prelevare campioni con una certa frequenza detta appunto frequenza di campionamento. Tale frequenza è individuata dall’intervallo di tempo che sceglieremo per prelevare i valori assunti dal nostro S(t). Il tempo di campionamento rappresenta questo intervallo e, d’ora in avanti, ci riferiremo ad esso con il nome Tc.
Chiaramente la frequenza di campionamento sarà:

Di qui, riferendoci al segnale campionato come Sc(t), esso sarà definito come l’insieme di campioni acquisiti in ogni intervallo Tc. Intendendo questo insieme di campioni come la somma di tanti impulsi che valgono 0 in ogni istante differente da quello in cui sono stati acquisiti e che in quell’istante assumono il valore del rispettivo segnale analogico, potremo asserire che il segnale campionato vale:

La funzione delta è denominata come delta di Dirac e rappresenta appunto la somma sopra citata.
Possiamo pensare la Sc(t) come il prodotto di due funzioni in cui una è il segnale analogico da campionare e l’altra è un treno di impulsi di area unitaria (C(nTc)), intervallata appunto di Tc unità:

Se ci riferiamo alla trasformata di Fourier dei segnali finora visti, allora potremo affermare che il nostro segnale campionato Sc(t), nel dominio di Fourier sarà quindi rappresentato da un insieme di repliche dello spettro del segnale iniziale S(t) spaziate tra loro di un intervallo pari a fc=1/Tc e scalate di un fattore pari ad 1/Tc.
La formula matematica che esprime questa trasformazione è:

che per le proprietà dell’impulso matematico diventa

Se lo spettro del segnale è limitato e non assume valori diversi da zero entro un intervallo fc (in questo caso si parla di segnale limitato in banda), allora risulta possibile ricostruire il segnale analogico di partenza (o eventualmente modificato dopo essere stato effettato o registrato) facendolo transitare in un filtro passa-basso che tagli le riproduzioni a frequenza superiore di quella base.

I problemi sorgono se invece il segnale non è limitato in banda fc/2: in tal caso le repliche dello spettro del segnale X(f) si sovrappongono e non è più possibile isolarlo dallo spettro Sc(f) e quindi ricostruire il segnale orginale da quello campionato.
Tale fenomeno è il famoso aliasing. In questo caso le repliche di S(f) sono molto distanziate tra loro ed `è possibile ricostruire il segnale originale S(t) utilizzando un filtro con specifiche molto meno restrittive del passa-basso ideale (e quindi anche fisicamente realizzabile).
Per questo nella pratica non si utilizzerà mai come frequenza di campionamento fc la frequenza di Nyquist, ma sempre frequenze superiori: l’importante è comunque non scendere al di sotto di tale limite per evitare fenomeni di distorsione dovuti all’aliasing.

Nella pratica come possiamo sapere a priori qual è la banda del segnale che si vuole campionare?
Per ovviare a questo problema si pone un filtro passa-basso in ingresso al campionatore: in questo modo conosciamo qual è la banda massima del segnale in ingresso, la banda del filtro passa-basso. Ovviamente tale filtro e la sua banda (e quindi la frequenza di campionamento), andranno scelti in modo da non distorcere il segnale di ingresso, ovvero ipotizzando quale potrebbe essere la banda massima del segnale in ingresso. Tali scelte vengono effettuate sulla base di studi statistici o analitici della natura del segnale che sappiamo di dover campionare (un segnale telefonico, un segnale vocale Hi-Fi, un segnale TV, il segnale in uscita dai nostri strumenti musicali, ecc.).
Gli strumenti in nostro possesso per garantire un discreto campionamento sono i filtri passa-basso, il convertitore analogico-digitale, i filtri antialiasing e via dicendo.
I vantaggi insiti nel campionamento riguardano il campo della manipolazione dei segnali ed il fatto di poter gestire i segnali stessi via software in modo sicuramente più economico e preciso rispetto all’applicazione di effetti e filtri direttamente sul segnale analogico.
Lo svantaggio principale nel campionamento dei segnali sta nel fatto che, in realtà, abbiamo a che fare con un’approssimazione (tanto migliore quanto il nostro tempo Tc è piccolo, ma pur sempre un’approssimazione) di quello che è il nostro ingresso. In questo modo il nostro segnale perde di “calore” e risulta timbricamente più freddo (un po’ la differenza che riscontriamo tra l’uso di un supporto come il vinile ed il cd).
Bene siamo al capolinea di questa lezione ^__^
Nei prossimi articoli ci occuperemo di fornire specifiche ed esempi di costruzione di convertitori analogici-digitali, filtri e quantizzatori. Stay Tuned MusicOffili ^__^










Aggiungi Commento